軟鋼線(軟らかい針金)の引張り試験をすると、どのような現象がおきるかを調べてみましょう。
図７はその結果で、縦は荷重(N)、横を伸びのたわみ(㎜)とすると、
・起点は０、
・A 点は前回(第五講)で勉強した弾性限(除荷によりたわみは０点まで戻る)で、
この点まで永久変形しません。
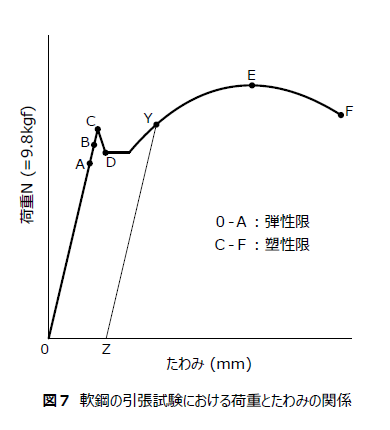A点を超えるとBCD曲線は複雑になりますが、このうち水平部のD点を降伏点と呼び、以下 DYEF とたわみは次第に伸びてF点で破断します。
一方、荷重は大きな変化はありませんが、弾性限以上となることは確かなようです。
このようにみると、０～A は弾性域、BCD 以上は塑性域と呼ぶことができます。
通常、ばねに用いるピアノ線はこのA 点(弾性限)を最大にしたものです。
フックの法則は図の0-A の範囲で、この間は直線で応力とたわみが一定です。これをヤング率(N/㎜2)といいます。
この弾性エネルギーの蓄積、及び解放を繰り返しても永久変形しないものをばねと定義することができます。
注）弾性エネルギー：物体に外力が作用して変形を生じ、これによって物体に吸収されるエネルギーをひずみエネルギーという。
弾性変形においてはひずみエネルギーはすべて一種の位置のエネルギーとして物体内に蓄えられます。
ひずみエネルギーEs(N・㎜)は
Es＝FS/２＝KS２ /2
このとき
F：ばねをひずませる力(N)
S：F によるばねのひずみ(㎜)
K：ばね定数(N/㎜）
材料の強度を表現するために引張り強さが高いことは、ばね材料として有利なことです。
それでは、ここに強度を知る目安となるいくつかの例を挙げてみましょう。
引張強さはσBで表します。
ねじり応力：τ 0.6＝τ/σB
弾性限…0.7σB （低温焼鈍前）
弾性限…0.8σB （低温焼鈍後）
静的なねじり許容応力 τalはそれぞれ、
・ピアノ線SWP・硬鋼線SW τal＝ 0.6×σal ＝ 0.6×(0.8×σB)＝ 0.48σB ≒ 0.5σＢ
・ステンレス鋼線 τal ≒ 0.45σB
・銅合金線 τal ≒ 0.4σB
硬さ(Hv)と引張強さ
σB ≒ Hv /３(kgf/㎜２)
注）この換算には JIS ハンドブックの参考欄にある硬さ換算表(SAE J417)を使用するとよい。
今日はこれまで。
